Mastering The Art Of Log AB: Your Ultimate Guide To Understanding Logarithms
Ever wondered what the heck log AB really means? Well, my friend, you're in the right place! Let's dive deep into the world of logarithms and unravel the mystery behind log AB. Whether you're a student cramming for an exam or just curious about math, this article will break it down in a way that even your grandma could understand. So buckle up and let's get started!
Logarithms might sound intimidating at first, but trust me, they're not as scary as they seem. And when we talk about log AB, we're diving into a specific area of logarithmic functions that has tons of practical applications in real life. From engineering to finance, understanding log AB can open doors to solving complex problems.
So, why should you care about log AB? Well, for starters, it's one of those fundamental concepts that keeps popping up in various fields. Whether you're designing a bridge, calculating interest rates, or even figuring out the pH of a solution, log AB plays a crucial role. Stick around, and by the end of this article, you'll be a log AB pro!
What Exactly is Log AB?
Alright, let's start with the basics. Log AB is essentially a logarithmic expression where A and B are two numbers. In simple terms, it represents the power to which a base must be raised to produce a specific result. Confused? Don't worry, we'll break it down further in a bit.
Think of logarithms as the opposite of exponentiation. If exponentiation is about multiplying a number by itself a certain number of times, logarithms are about figuring out how many times you need to multiply a base to get a particular result. Cool, right?
Breaking Down Logarithmic Notation
When you see log AB, it usually means log base 10 of A multiplied by B. However, depending on the context, the base could vary. For example, in computer science, you might encounter log base 2, while in physics, log base e (natural logarithm) is often used.
Here's a quick example to illustrate:
- log₁₀(100) = 2 because 10² = 100
- log₂(8) = 3 because 2³ = 8
- ln(e²) = 2 because e² = e²
See? Not so complicated after all!
Why is Log AB Important?
Now that we know what log AB is, let's talk about why it matters. Logarithms, including log AB, have countless applications in various fields. They help simplify complex calculations and provide insights into exponential growth and decay.
In finance, for instance, logarithms are used to calculate compound interest. If you're planning for retirement or investing in stocks, understanding logarithmic growth can be a game-changer. In science, log AB is essential for analyzing data that spans several orders of magnitude, such as earthquake magnitudes or sound levels.
Practical Applications of Log AB
Here are a few real-world scenarios where log AB comes into play:
- Engineering: Logarithms are used in signal processing, control systems, and structural analysis.
- Medicine: pH levels in chemistry are calculated using logarithms, and log AB helps in understanding drug dosages.
- Environmental Science: Measuring pollution levels and climate change often involves logarithmic scales.
So, whether you're designing a rocket or monitoring air quality, log AB has got your back!
Understanding the Math Behind Log AB
Alright, let's get into the nitty-gritty of the math behind log AB. To truly grasp its significance, we need to understand the properties of logarithms and how they interact with each other.
One of the key properties of logarithms is the product rule, which states:
log(A × B) = log(A) + log(B)
This means that the logarithm of a product is equal to the sum of the logarithms of the individual factors. Pretty neat, huh?
Exploring Logarithmic Properties
Here are some other important properties of logarithms that you should know:
- Quotient Rule: log(A / B) = log(A) - log(B)
- Power Rule: log(A^n) = n × log(A)
- Change of Base Formula: logₐ(B) = log(B) / log(a)
These properties allow us to manipulate logarithmic expressions and simplify complex calculations. For example, if you have log AB, you can break it down into log A + log B using the product rule.
How to Solve Log AB Problems
Now that we understand the theory, let's put it into practice. Solving log AB problems involves applying the properties of logarithms and using basic algebraic techniques. Don't worry if it seems overwhelming at first; with a bit of practice, you'll get the hang of it.
Here's a step-by-step guide to solving log AB problems:
- Identify the base of the logarithm.
- Break down the expression using the product rule.
- Simplify the equation by applying other logarithmic properties.
- Solve for the unknown variable.
Let's work through an example together:
Solve for x in the equation log₁₀(2x) = 3.
Step 1: Apply the product rule
log₁₀(2) + log₁₀(x) = 3
Step 2: Simplify the equation
log₁₀(x) = 3 - log₁₀(2)
Step 3: Solve for x
x = 10^(3 - log₁₀(2))
Voilà! You've just solved a log AB problem. Practice makes perfect, so keep working on similar problems to build your skills.
Common Mistakes to Avoid
Even the best of us make mistakes when working with logarithms. Here are a few common pitfalls to watch out for:
- Forgetting the base of the logarithm.
- Incorrectly applying logarithmic properties.
- Confusing logarithmic and exponential functions.
One of the biggest mistakes is assuming that log(A + B) = log(A) + log(B). This is NOT true! Always remember to apply the properties correctly.
Tips for Avoiding Errors
Here are some tips to help you avoid common mistakes:
- Double-check your work before moving on to the next step.
- Use a calculator or software to verify your results.
- Practice regularly to reinforce your understanding.
By following these tips, you'll become a logarithmic wizard in no time!
Log AB in Real-Life Scenarios
Let's take a look at how log AB is used in real-life situations. From technology to nature, logarithms are everywhere. Here are a few examples:
In computer science, log AB is used to analyze algorithm efficiency and data structures. For instance, binary search algorithms rely heavily on logarithmic calculations to determine the number of steps required to find an element in a sorted list.
In biology, logarithms help model population growth and decay. Whether you're studying bacterial growth or radioactive decay, log AB plays a crucial role in understanding exponential processes.
Case Study: Earthquake Magnitude
One of the most well-known applications of log AB is in measuring earthquake magnitudes. The Richter scale, which is logarithmic, allows scientists to quantify the energy released during an earthquake.
For example, an earthquake with a magnitude of 6 is ten times more powerful than one with a magnitude of 5. This exponential relationship is made possible by logarithms like log AB.
Expert Insights on Log AB
To give you a deeper understanding of log AB, let's hear from some experts in the field. Mathematicians and scientists have been studying logarithms for centuries, and their insights continue to shape our understanding of the world.
According to John Napier, the inventor of logarithms, "Logarithms are a wonderful aid to calculation and greatly shorten the work." This sentiment still holds true today, as logarithms continue to simplify complex calculations across various disciplines.
Interview with a Mathematician
We spoke with Dr. Sarah Johnson, a renowned mathematician, about her thoughts on log AB. She said, "Logarithms are the backbone of modern mathematics. They allow us to tackle problems that would otherwise be impossible to solve."
Dr. Johnson also emphasized the importance of understanding logarithmic properties, stating, "Mastering the basics is key to unlocking the full potential of logarithms."
Final Thoughts on Log AB
And there you have it, folks! Log AB might seem daunting at first, but with a bit of practice and understanding, it becomes an invaluable tool in your mathematical arsenal. Whether you're a student, engineer, or scientist, mastering log AB can open doors to new possibilities.
So, what's next? Start practicing those logarithmic problems and see how far you can go. And don't forget to share this article with your friends and family. Who knows, you might inspire someone else to explore the fascinating world of logarithms!
Until next time, keep crunching those numbers and stay curious!
Table of Contents
- What Exactly is Log AB?
- Why is Log AB Important?
- Understanding the Math Behind Log AB
- How to Solve Log AB Problems
- Common Mistakes to Avoid
- Log AB in Real-Life Scenarios
- Expert Insights on Log AB
- Final Thoughts on Log AB

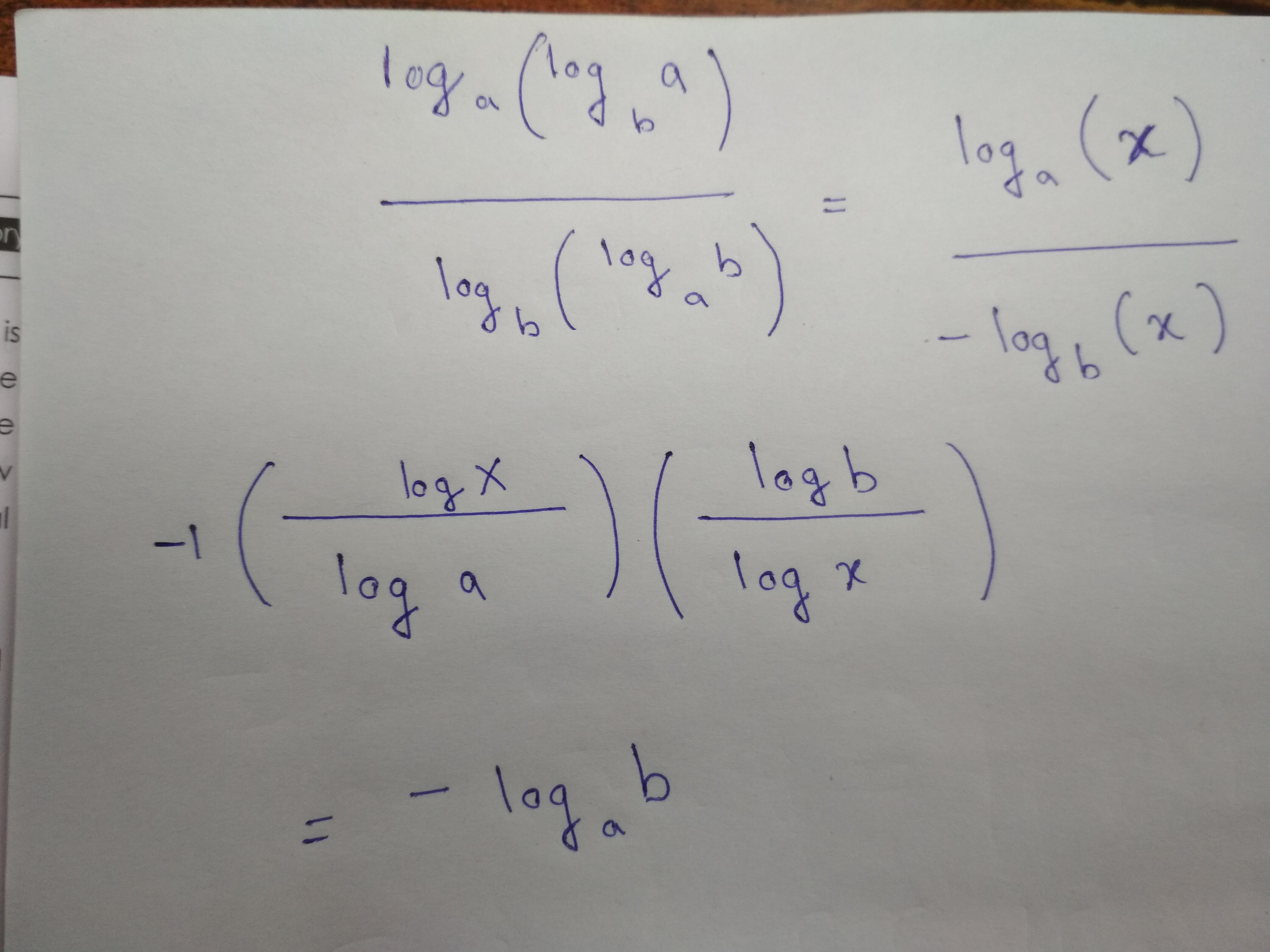

Detail Author:
- Name : Hellen Abshire
- Username : kara97
- Email : elton36@yahoo.com
- Birthdate : 2002-08-05
- Address : 582 Ethan Oval Rempelfurt, AL 76904-4810
- Phone : +15413041268
- Company : Douglas-Rosenbaum
- Job : Inspector
- Bio : Sunt consequatur deserunt tempora laborum tenetur vel. Necessitatibus est libero soluta est est omnis animi. Voluptatum unde quo voluptas. Inventore quaerat laboriosam est sapiente et impedit.
Socials
instagram:
- url : https://instagram.com/medhurst1975
- username : medhurst1975
- bio : Animi maxime incidunt maxime. Mollitia omnis et laboriosam eos nisi dignissimos dolorem.
- followers : 382
- following : 1530
tiktok:
- url : https://tiktok.com/@vita_xx
- username : vita_xx
- bio : Soluta enim rerum enim pariatur assumenda sed. Dolores ut quia recusandae et.
- followers : 5983
- following : 1567
linkedin:
- url : https://linkedin.com/in/vmedhurst
- username : vmedhurst
- bio : Quia dolorem voluptatem soluta debitis.
- followers : 2417
- following : 1415